有界函式f(x)黎曼可積的充要條件是f(x)幾乎處處連續。
而狄利克雷函式:
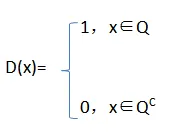
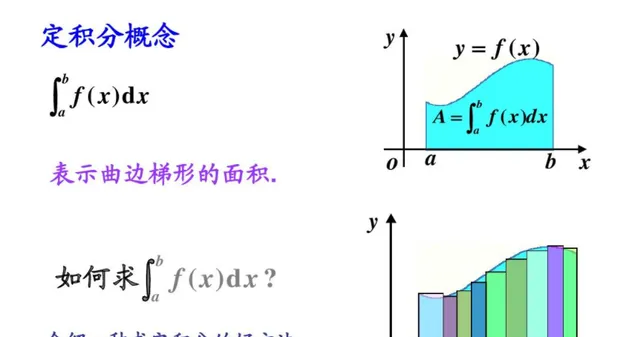
黎曼積分的過程就是把自變量區間劃分成一個個無窮小區間之和。然後在這個無窮小區間Δx的範圍內, 所有的點對應的函式值都相同 ,即可以得到一個矩形面積:
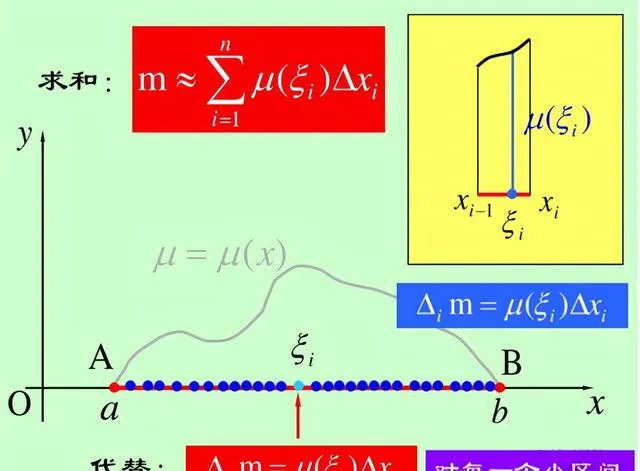
這種情況對於函式連續的情形是沒有問題的。所謂函式連續,就是當這個函式的自變量幾乎不變的時候,這個函式的函式值也幾乎不變化,而幾乎不變化就是這種變化是無窮小。
但問題在於,自變量劃分的任意一個區間,包括無窮小區間,都有有理點和無理點:
上圖表示,在x劃分的一個無窮小區間內,存在一個有理數點和無數個無理數點。
而根據狄利克雷函式的定義,在這個無窮小區間內,因為 有理數點和無理數點所對應的函式值不相等 ,因此也就無法得到一個矩形,從而計算出這個無窮小區間內的面積,所以狄利克雷函式是黎曼不可積分的。
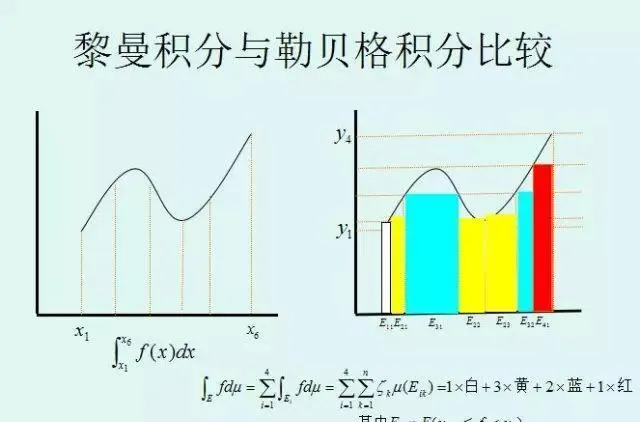
那狄利克雷函式為什麽又是勒貝格可積分的呢?
原因就在於,勒貝格積分是把有理數點和無理數點分開計算的。
既然有理數和無理數對應的函式值不相同,那就先計算所有有理數點的長度,再把這個長度乘以有理數點對應的函式值,不就得到所有有理數點所構成的面積了嗎?然後對無理數點也采取相同的方法,這樣處理以後,狄利克雷函式的積分不就可以計算出來了嗎?
當然,狄利克雷函式中因為所有有理數點構成的集合其長度(測度)為0,雖然其函式值等於1,其積分結果還是0;雖然所有無理數點構成的集合其長度(測度)不等於0,但其函式值等於0,所有其積分結果也是0。由此,狄利克雷函式的整個勒貝格積分的結果等於0。
簡單來說:
1:黎曼積分可積分的條件就是在自變量的一個無窮小區間內,其對應的函式值必須相等;
2:但自變量的任一個無窮小區間內既包含有理數也包含無理數;
3:狄利克雷函式的定義剛好破壞了黎曼可積分的條件;
4:勒貝格積分則是把有理數點和無理數點分開考慮,這種分開的方法使得狄利克雷函式的積分變得可以計算。











