有界函数f(x)黎曼可积的充要条件是f(x)几乎处处连续。
而狄利克雷函数:
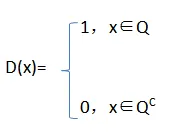
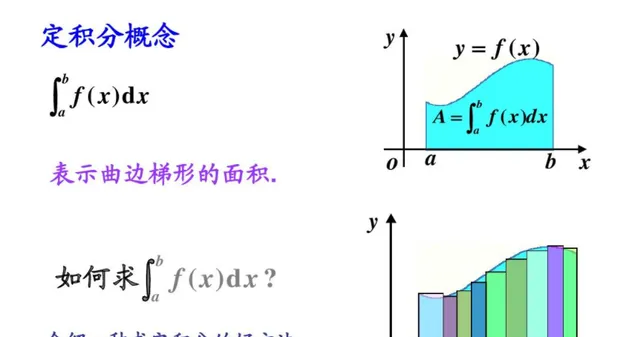
黎曼积分的过程就是把自变量区间划分成一个个无穷小区间之和。然后在这个无穷小区间Δx的范围内, 所有的点对应的函数值都相同 ,即可以得到一个矩形面积:
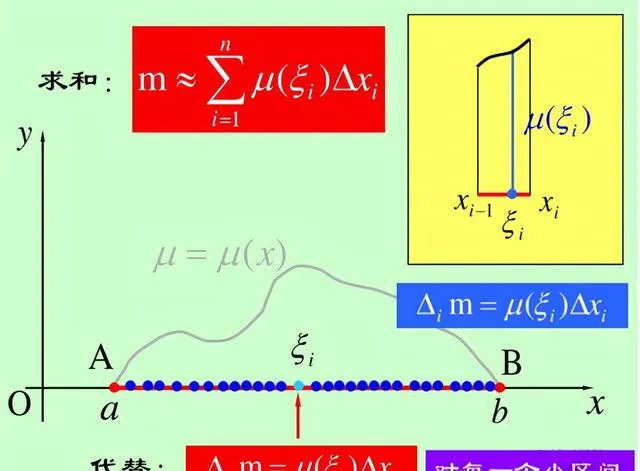
这种情况对于函数连续的情形是没有问题的。所谓函数连续,就是当这个函数的自变量几乎不变的时候,这个函数的函数值也几乎不变化,而几乎不变化就是这种变化是无穷小。
但问题在于,自变量划分的任意一个区间,包括无穷小区间,都有有理点和无理点:
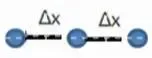
上图表示,在x划分的一个无穷小区间内,存在一个有理数点和无数个无理数点。
而根据狄利克雷函数的定义,在这个无穷小区间内,因为 有理数点和无理数点所对应的函数值不相等 ,因此也就无法得到一个矩形,从而计算出这个无穷小区间内的面积,所以狄利克雷函数是黎曼不可积分的。
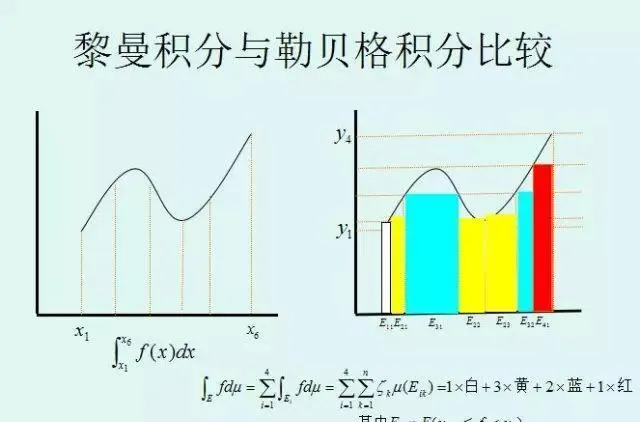
那狄利克雷函数为什么又是勒贝格可积分的呢?
原因就在于,勒贝格积分是把有理数点和无理数点分开计算的。
既然有理数和无理数对应的函数值不相同,那就先计算所有有理数点的长度,再把这个长度乘以有理数点对应的函数值,不就得到所有有理数点所构成的面积了吗?然后对无理数点也采取相同的方法,这样处理以后,狄利克雷函数的积分不就可以计算出来了吗?
当然,狄利克雷函数中因为所有有理数点构成的集合其长度(测度)为0,虽然其函数值等于1,其积分结果还是0;虽然所有无理数点构成的集合其长度(测度)不等于0,但其函数值等于0,所有其积分结果也是0。由此,狄利克雷函数的整个勒贝格积分的结果等于0。
简单来说:
1:黎曼积分可积分的条件就是在自变量的一个无穷小区间内,其对应的函数值必须相等;
2:但自变量的任一个无穷小区间内既包含有理数也包含无理数;
3:狄利克雷函数的定义刚好破坏了黎曼可积分的条件;
4:勒贝格积分则是把有理数点和无理数点分开考虑,这种分开的方法使得狄利克雷函数的积分变得可以计算。











