Serre對偶定理:復流形上的全純向量叢與餘調群
Serre對偶定理是復幾何和代數幾何中的一個核心概念,它建立了緊致復流形上全純向量叢的餘調群之間的深刻聯系。這一定理不僅為我們提供了一種計算全純向量叢的餘調群的有效方法,還揭示了復流形上幾何結構與代數性質之間的微妙關系。
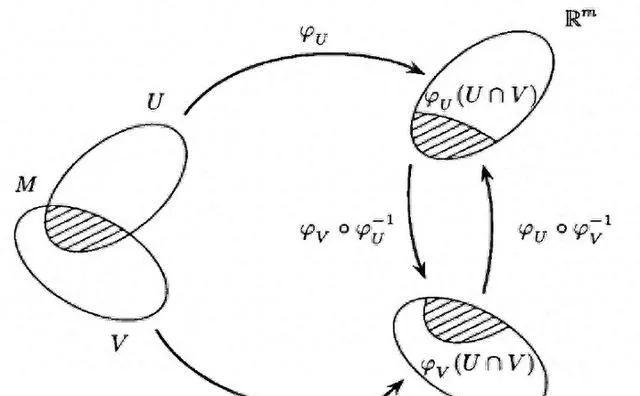
緊致復流形與全純向量叢
緊致復流形是復分析中的一類重要物件,它們是在復數體上定義的、具有緊致拓撲結構的流形。全純向量叢則是流形上的一種幾何結構,它為流形的每一點都賦予了一個復數向量空間,並且這些向量空間在流形上平滑地變化。
Serre對偶定理的陳述
根據Serre對偶定理,對於緊致復流形X上的任意整數k和兩個全純向量叢E、F,存在一個自然的同構:
H^k(X, E ⊗ Ω^n_X) ≅ H^{n-k}(X, E^* ⊗ F)
其中,H^k(X, E ⊗ Ω^n_X)表示X上關於E與X的全純n-形式叢Ω^n_X的張量積的上k階Dolbeault餘調群;E*是E的對偶叢;Ω^n_X是X上的全純n-形式叢,即X上所有全純n-形式的集合;⊗表示向量叢的張量積。
定理的幾何意義

Serre對偶定理的幾何意義在於它揭示了復流形上全純向量叢的餘調群之間的對偶關系。這種對偶關系在數學和物理學中都扮演著重要角色,尤其是在弦論和量子場論中,它為我們提供了一種理解和描述復雜系統的新視角。
定理的套用
Serre對偶定理在復幾何和代數幾何中有著廣泛的套用。例如,在代數幾何中,我們可以利用該定理研究代數曲線和代數曲面上的全純向量叢的性質,從而得到關於這些曲線和曲面的重要資訊。此外,該定理還可以用於計算全純向量叢的餘調群,這對於理解復流形的幾何結構和拓撲性質具有重要意義。
結論
總的來說,Serre對偶定理是復幾何和代數幾何中的一個基本而重要的定理。它不僅為我們提供了一種計算全純向量叢的餘調群的有效方法,還揭示了復流形上幾何結構與代數性質之間的深刻聯系。透過深入研究和套用這一定理,我們可以更好地理解和描述復流形及其上的全純向量叢的幾何結構和拓撲性質,從而為數學和物理學中的其他領域提供有力支持。











