一维量子XY模型与Jordan-Wigner变换
Jordan-Wigner变换是求解某些一维量子自旋模型的有力方法,它对于我们理解一维自旋系统的一般特征是很有价值的。当然,除了一维自旋体系,部分二维自旋系统也可以用Jordan-Wigner变换求解,例如著名的Kitaev honeycomb模型,关于其求解在我们先前的文章中已经介绍,感兴趣的读者可以参考:
让我们考虑一维量子XY模型,其描述x与y方向的自旋交换耦合.
\begin{equation} \hat{H}_{XY}=-J\sum_{j}[\hat{S}_{j}^{x}\hat{S}_{j+1}^{x}+\hat{S}_{j}^{y}\hat{S}_{j+1}^{y}]=-\frac{J}{2}\sum_{j}[\hat{S}_{j}^{+}\hat{S}_{j+1}^{-}+\hat{S}_{j}^{-}\hat{S}_{j+1}^{+}] \end{equation}
这里的自旋 1/2 算符满足 SU(2) 对易关系 [\hat{S}_{j}^{\alpha},\hat{S}_{k}^{\beta}]=i\varepsilon^{\alpha\beta\gamma}\delta_{jk}\hat{S}_{k}^{\gamma} . 注意到与具有完全自旋 SU(2) 旋转对称的Heisenberg模型相比,这里少了 z 方向的耦合
\begin{equation} -J\sum_{j}\hat{S}_{j}^{z}\hat{S}_{j+1}^{z} \end{equation}
换句话说,体系的对称性从 SU(2) 减少到 U(1) 或 O(2) . [1]
单个S=1/2自旋的费米子表示
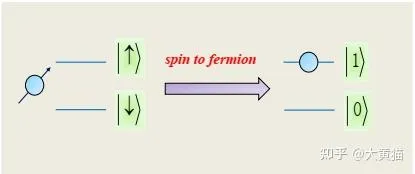
对于一个孤立的S=1/2自旋,其Hilbert空间与一个无自旋费米子是相似的,这提示我们自旋与费米子之间可能有如下对应关系:
\begin{equation} |\downarrow\rangle\leftrightarrow |0\rangle,~~|\uparrow\rangle\leftrightarrow |1\rangle=\hat{f}^{\dag}|0\rangle \end{equation}
也就是说我们可以把自旋的下态对应没有费米子的状态,而自旋上态对应有一个费米子的状态.那么相应的算符也有如下的对应 [2]
\begin{equation} \hat{S}^{+}=\hat{f}^{\dag},~~\hat{S}^{-}=\hat{f},~~\hat{S}^{z}=\hat{f}^{\dag}\hat{f}-\frac{1}{2}. \end{equation}
让我们检验自旋算符间的对易或反对易关系是否能够由上述费米子表示来实现.首先,我们知道,对于S=1/2自旋有 (\hat{S}^{x})^{2}=(\hat{S}^{y})^{2}=(\hat{S}^{z})^{2}=\frac{1}{4} 或者说 \hat{\vec{S}}\cdot\hat{\vec{S}}=\frac{3}{4}.而由\hat{S}^{\pm}=\hat{S}^{x}\pm i\hat{S}^{y} 可得
\begin{equation} \hat{S}^{x}=\frac{1}{2}(\hat{S}^{+}+\hat{S}^{-})=\frac{1}{2}(\hat{f}^{\dag}+\hat{f}), ~\hat{S}^{y}=\frac{1}{2i}(\hat{S}^{+}-\hat{S}^{-})=\frac{1}{2i}(\hat{f}^{\dag}-\hat{f}). \end{equation}
这样就有
\begin{equation} (\hat{S}^{x})^{2}=\frac{1}{4}(\hat{f}^{\dag}+\hat{f})(\hat{f}^{\dag}+\hat{f})=\frac{1}{4}\{\hat{f}^{\dag},\hat{f}\}=\frac{1}{4}. \end{equation}
注意到我们(将会)大量使用费米子算符自乘为零这一性质,即 \hat{f}^{\dag}\hat{f}^{\dag}=\hat{f}\hat{f}=0 以及费米子的反对易关系 \{\hat{f}^{\dag},\hat{f}\}=\hat{f}\hat{f}^{\dag}+\hat{f}^{\dag}\hat{f}=1 .类似的,我们发现 (\hat{S}^{y})^{2}=\frac{1}{4i^{2}}(-1)\{\hat{f}^{\dag},\hat{f}\}=\frac{1}{4} ,
\begin{equation} (\hat{S}^{z})^{2}=\left(\hat{f}^{\dag}\hat{f}-\frac{1}{2}\right)\left(\hat{f}^{\dag}\hat{f}-\frac{1}{2}\right) =\overbrace{\hat{f}^{\dag}\hat{f}\hat{f}^{\dag}\hat{f}}^{=\hat{f}^{\dag}\hat{f}}-\hat{f}^{\dag}\hat{f}+\frac{1}{4}=\frac{1}{4}. \end{equation}
因此,自旋算符平方为 1/4 确实可用费米子完全表示.接下来, \hat{S}^{x},\hat{S}^{y} 的对易关系是
\begin{eqnarray} [\hat{S}^{x},\hat{S}^{y}]=\frac{1}{4i}[\hat{f}^{\dag}+\hat{f},\hat{f}^{\dag}-\hat{f}]=\frac{1}{2i}(1-2\hat{f}^{\dag}\hat{f})=i\hat{S}^{z}. \end{eqnarray}
\hat{S}^{y},\hat{S}^{z} 的对易关系是
\begin{eqnarray} [\hat{S}^{y},\hat{S}^{z}]=\frac{1}{2i}[\hat{f}^{\dag}-\hat{f},\hat{f}^{\dag}\hat{f}]=-\frac{1}{2i}(\hat{f}\hat{f}^{\dag}\hat{f}+\hat{f}^{\dag}\hat{f}\hat{f}^{\dag}) =-\frac{1}{2i}(\hat{f}+\hat{f}^{\dag})=i\hat{S}^{x}.\nonumber \end{eqnarray}
显然,费米子表示也可以得到正确的自旋对易关系.最后,让我们自旋间的反对以关系也可用费米子成功表示,即
\begin{equation} \{\hat{S}^{x},\hat{S}^{y}\}=\frac{1}{4i}\{\hat{f}^{\dag}+\hat{f},\hat{f}^{\dag}-\hat{f}\}=0. \end{equation}
\begin{equation} \{\hat{S}^{y},\hat{S}^{z}\}=\frac{1}{2i}\{\hat{f}^{\dag}-\hat{f},\hat{f}^{\dag}\hat{f}-1/2\}= \frac{1}{2i}(-\hat{f}-\hat{f}^{\dag}+\hat{f}\hat{f}^{\dag}\hat{f}+\hat{f}^{\dag}\hat{f}\hat{f}^{\dag})= \frac{1}{2i}(-\hat{f}-\hat{f}^{\dag}+\hat{f}+\hat{f}^{\dag})=0. \end{equation}
两个S=1/2自旋的费米子表示
在用费米子成功表示单个S=1/2自旋后,让我们考虑多个自旋的情况,例如两个自旋, \hat{\vec{S}}_{1},\hat{\vec{S}}_{2} .我们知道,不同自旋之间是互相对易的,如果直接套用单个自旋的费米子表示,(j=1,2)
\begin{equation} \hat{S}^{x}_{j}=\frac{1}{2}(\hat{f}^{\dag}_{j}+\hat{f}_{j}), ~\hat{S}^{y}_{j}=\frac{1}{2i}(\hat{f}^{\dag}_{j}-\hat{f}_{j}),~\hat{S}^{z}_{j}=\hat{f}^{\dag}_{j}\hat{f}_{j}-\frac{1}{2} \end{equation}
那么会发现,
\begin{eqnarray} [\hat{S}^{x}_{1},\hat{S}^{y}_{2}]&=&\frac{1}{4i}[\hat{f}^{\dag}_{1}+\hat{f}_{1},\hat{f}^{\dag}_{2}-\hat{f}_{2}]\nonumber\\ &=&\frac{1}{4i}[\overbrace{(\hat{f}^{\dag}_{1}\hat{f}^{\dag}_{2}-\hat{f}^{\dag}_{1}\hat{f}_{2}+\hat{f}_{1}\hat{f}^{\dag}_{2}-\hat{f}_{1}\hat{f}_{2})}^{\hat{W}_{12}}- (\overbrace{\hat{f}^{\dag}_{2}\hat{f}^{\dag}_{1}-\hat{f}^{\dag}_{2}\hat{f}_{1}+\hat{f}_{2}\hat{f}^{\dag}_{1}-\hat{f}_{2}\hat{f}_{1})}^{\hat{W}_{21}}]\neq0.\nonumber \end{eqnarray}
可以看到,上式中 \hat{W}_{12},\hat{W}_{21}(\hat{W}_{12}=-\hat{W}_{21}) 因为对易关系本身的负号而无法抵消.这说明简单的推广单个自旋的费米子表示不能正确反映不同自旋间的对易关系.注意到如果因为某种原因,我们可以给 \hat{W}_{21} 前面再添加上一个负号,那么 \hat{W}_{12}+(-1)^{2}\hat{W}_{21}=0 .所以,我们需要寻找一种方案,使得不同自旋之间做对易关系时出现一个负号,历史上,这个关系由Jordan和Wigner发现,即所谓的Jordan-Wigner变换. [3]
Jordan-Wigner变换
考虑定义在晶格格点上的自旋,由于每个格点间的自旋是对易的(每个格点的自旋是可分辨的),因此我们需要额外的东西来确保不同格点自旋的对易性.注意到费米子之间反对易,因此需要添加的可以是一个产生额外负号的相位因子部分,对一维自旋系统而言,Jordan-Wigner变换明确给出S=1/2系统与费米子系统的对应:
\begin{eqnarray} \boxed{\hat{S}_{j}^{+}=\hat{f}_{j}^{\dag}e^{i\hat{\phi}_{j}},~~\hat{\phi}_{j}=\pi\sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m},~~\hat{S}_{j}^{z}=\hat{f}_{j}^{\dag}\hat{f}_{j}-\frac{1}{2}} \end{eqnarray}
这里 \hat{S}_{j}^{+},\hat{S}_{j}^{z} 是第 j 个(格点)的 S=1/2 自旋算符,满足标准的对易关系 [\hat{S}_{j}^{x},\hat{S}_{k}^{y}]=i\delta_{j,k}\hat{S}_{j}^{z}.\hat{f}^{\dag}_{j},\hat{f}_{j} 是标准的费米子算符,满足反对易关系 \{\hat{f}_{j},\hat{f}_{k}^{\dag}\}=\delta_{j,k} .相因子部分 e^{i\hat{\phi}_{j}}=e^{i\pi\sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m}}=e^{i\pi\sum_{1\leq m<j}(\hat{S}_{m}^{z}+1/2)} 称为Jordan-Wigner弦(算符),其与 \hat{f}_{j}^{\dag},\hat{f}_{j} 都是对易的.Jordan-Wigner弦物理意义是 j 格点的自旋算符感受到其他自旋对其的相位调制.
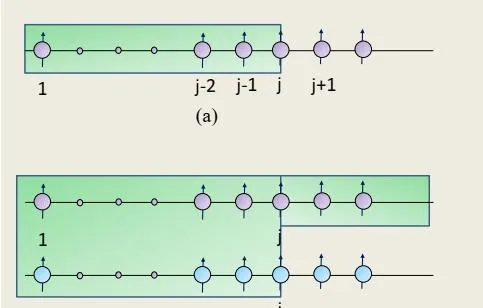
在一维链的情况下, j 格点的相位 \phi_{j} 依赖于第一个到 j-1 格点的费米子的占据数 \sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m} ,每存在一个费米子就会贡献一个相位 \pi ,总的相位便是所有 j 格点左侧格点的相位之和.
在实际使用中,我们注意到
\begin{equation} e^{i\pi\hat{f}_{m}^{\dag}\hat{f}_{m}}=(-1)^{\hat{f}_{m}^{\dag}\hat{f}_{m}}=1-2\hat{f}_{m}^{\dag}\hat{f}_{m} \end{equation}
比较上式两边的本征值就可证明这个关系.另外,
\begin{equation} \hat{S}_{j}^{-}=\hat{f}_{j}e^{-i\hat{\phi}_{j}}=\hat{f}_{j}e^{i\hat{\phi}_{j}}. \end{equation}
也就是说 e^{-i\hat{\phi}_{j}}=e^{i\hat{\phi}_{j}} .这样 e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{j}}=e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}=1 .
\begin{equation} \hat{S}_{j}^{x}=\frac{1}{2}(\hat{S}_{j}^{+}+\hat{S}_{j}^{-})=\frac{1}{2}(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}. \end{equation}
\begin{equation} \hat{S}_{j}^{y}=\frac{1}{2i}(\hat{S}_{j}^{+}-\hat{S}_{j}^{-})=\frac{1}{2i}(\hat{f}_{j}^{\dag}-\hat{f}_{j})e^{i\hat{\phi}_{j}}. \end{equation}
反过来,我们也可以用自旋来表示费米子,即有
\begin{equation} \hat{f}_{j}^{\dag}=\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}=\hat{S}_{j}^{+}\prod_{m<j}\hat{R}_{m}(\vec{e}_{z},\pi)e^{i\pi(j-1)/2} \end{equation}
注意到自旋旋转算符 \hat{R}_{m}(\vec{e}_{z},\pi) 会使得 \hat{S}_{m}^{x}\rightarrow-\hat{S}_{m}^{x},\hat{S}_{m}^{y}\rightarrow-\hat{S}_{m}^{y} ,这样当费米子算符 \hat{f}_{j}^{\dag} 作用于 |\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow...\rangle 得到 |\leftarrow\leftarrow\leftarrow\rightarrow\rightarrow\rightarrow...\rangle ,也就是相对于自旋取向均为 S^{x}=1/2 的态产生一个在 j 处的畴壁.这说明费米子算符就是畴壁的产生或者湮灭算符,即XY模型中的畴壁是费米子.
为了讨论的完整性,让我们验证自旋算符满足想要的对易关系.对于同一个格点的自旋,Jordan-Wigner弦算符互相抵消,因此其对易关系与单个 S=1/2 自旋是一致的.对于不同格点自旋,例如 \hat{S}_{j}^{x},\hat{S}_{k}^{y} (设 j<k )的对易关系:
\begin{eqnarray} [\hat{S}^{x}_{j},\hat{S}^{y}_{k}]&=&\frac{1}{4i}[(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}},(\hat{f}_{k}^{\dag}-\hat{f}_{k})e^{i\hat{\phi}_{k}}]\nonumber\\ &=&\frac{1}{4i}\left((\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}(\hat{f}_{k}^{\dag}-\hat{f}_{k}) -(\hat{f}_{k}^{\dag}-\hat{f}_{k})e^{i\hat{\phi}_{k}}e^{i\hat{\phi}_{j}}(\hat{f}_{j}^{\dag}+\hat{f}_{j})\right).\nonumber \end{eqnarray}
注意到
\begin{equation} e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}=e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}e^{i\pi \hat{f}_{j}^{\dag}f_{j}}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(1-2\hat{f}_{j}^{\dag}f_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}. \end{equation}
那么
\begin{eqnarray} (\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}= (\hat{f}_{j}^{\dag}+\hat{f}_{j})(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(\hat{f}_{j}^{\dag}-\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}.\nonumber \end{eqnarray}
另一方面,
\begin{eqnarray} e^{i\hat{\phi}_{k}}e^{i\hat{\phi}_{j}}(\hat{f}_{j}^{\dag}+\hat{f}_{j}) =(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(\hat{f}_{j}-\hat{f}_{j}^{\dag})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}.\nonumber \end{eqnarray}
所以
\begin{eqnarray} [\hat{S}^{x}_{j},\hat{S}^{y}_{k}]&=&\frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}\left((\hat{f}_{j}^{\dag}-\hat{f}_{j})(\hat{f}_{k}^{\dag}-\hat{f}_{k}) -(\hat{f}_{k}^{\dag}-\hat{f}_{k})(\hat{f}_{j}-\hat{f}_{j}^{\dag})\right)\nonumber\\ &=& \frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}\left((\hat{f}_{j}^{\dag}-\hat{f}_{j})(\hat{f}_{k}^{\dag}-\hat{f}_{k}) +(-1)^{2}(\hat{f}_{k}^{\dag}-\hat{f}_{k})(\hat{f}_{j}^{\dag}-\hat{f}_{j})\right)\nonumber\\ &=&\frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}} \left( \{\hat{f}_{j}^{\dag},\hat{f}_{k}^{\dag}\} -\{\hat{f}_{j}^{\dag},\hat{f}_{k}\} -\{\hat{f}_{j},\hat{f}_{k}^{\dag}\} +\{\hat{f}_{j},\hat{f}_{k}\}\right)=0.\nonumber \end{eqnarray}
最后,容易发现,
\begin{equation} [\hat{S}_{j}^{y},\hat{S}_{k}^{z}]=\frac{1}{2i}e^{i\hat{\phi}_{j}}[\hat{f}^{\dag}_{j}-\hat{f}_{j},\hat{f}^{\dag}_{k}\hat{f}_{k}]=0.\nonumber \end{equation}
总的来说,我们发现引入Jordan-Wigner变换,(更明确的说是引入Jordan-Wigner弦)可以实现不同格点自旋间的对易关系.
用Jordan-Wigner变换求解XY模型
把Jordan-Wigner变换代入XY模型可以得到
\begin{eqnarray} \hat{H}_{XY}&=&-\frac{J}{2}\sum_{j}[\hat{S}_{j}^{+}\hat{S}_{j+1}^{-}+\hat{S}_{j}^{-}\hat{S}_{j+1}^{+}]\\ &=&-\frac{J}{2}\sum_{j}[\hat{f}_{j}^{\dag}e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})\hat{f}_{j+1}+H.c.]\\ &=&-\frac{J}{2}\sum_{j}[\hat{f}_{j}^{\dag}\hat{f}_{j+1}+\hat{f}_{j+1}^{\dag}\hat{f}_{j}] \end{eqnarray}
这样我们发现一维量子XY模型已经变换为一维自由无自旋费米子系统.
现在,让我们假设体系具有周期边界条件,这意味着边界上的最后一个自旋 \hat{S}^{\pm}_{N_{s}} (假设体系有 N_{s} 个格点)与第一个自旋 \hat{S}_{1}^{\pm} 具有相互作用
\begin{eqnarray} \hat{H}_{PBC}=-\frac{J}{2}[\hat{S}_{N_{s}}^{+}\hat{S}_{1}^{-}+\hat{S}_{N_{s}}^{-}\hat{S}_{1}^{+}]&=& -\frac{J}{2}e^{i\pi\sum_{m=1}^{N_{s}-1}\hat{f}_{m}^{\dag}\hat{f}_{m}}[\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]\nonumber\\ &=&-\frac{J}{2}e^{i\pi \hat{N}_{f}}e^{i\pi\hat{f}_{N_{s}}^{\dag}\hat{f}_{N_{s}}}[\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]\nonumber\\ &=&-\frac{J}{2}(-1)^{\hat{N}_{f}}[-\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]. \end{eqnarray}
这里我们定义了总费米子数算符 \hat{N}_{f}=\sum_{m=1}^{N_{s}}\hat{f}_{m}^{\dag}\hat{f}_{m} .注意到 \hat{N}_{f} 是守恒量,那么 (-1)^{\hat{N}_{f}} 可以为 1 或 -1 ,前者对应 \hat{N}_{f} 为偶数,后者对应 \hat{N}_{f} 为奇数.当 \hat{N}_{f} 为偶数时, (-1)^{\hat{N}_{f}}=1 ,为了使 \hat{H}_{PBC} 具有 \hat{H}_{XY} 的形式,可以设 \hat{f}_{1}=-\hat{f}_{N_{s}+1} .同理,当 \hat{N}_{f} 为奇数时, (-1)^{\hat{N}_{f}}=-1 ,我们可设 \hat{f}_{1}=\hat{f}_{N_{s}+1} .因此,我们发现总费米子数的奇偶性决定了费米子满足周期( \hat{f}_{1}=\hat{f}_{N_{s}+1} )或反周期( \hat{f}_{1}=-\hat{f}_{N_{s}+1} )边界条件.
定义费米子的傅里叶变换为 \hat{f}_{j}=\frac{1}{\sqrt{N_{s}}}\sum_{k}e^{ikR_{j}}\hat{f}_{k} ,对于周期边界我们发现( R_{j}=ja,a 为晶格间距,可设为1)
\begin{equation} \hat{f}_{1}=\hat{f}_{N_{s}+1}\Rightarrow e^{ika}=e^{ik(R_{N_{s}}+a)}\Rightarrow e^{ikN_{s}}=1 \end{equation}
这说明动量 k 可以取 k=\frac{2\pi}{N_{s}}n (n 取所有整数,即 n=0,\pm1,\pm2... ).另一方面,对于反周期边界则有
\begin{equation} \hat{f}_{1}=-\hat{f}_{N_{s}+1}\Rightarrow e^{ikN_{s}}=-1 \end{equation}
这样 k=\frac{2\pi}{N_{s}}n ( n 取所有半整数,即 n=\pm1/2,\pm3/2... ).因此,我们看到周期与反周期边界条件实际上会影响动量 k 的取值,当然,在热力学极限下 N_{s}\rightarrow\infty ,动量的取值足够密集,此时两者的区别可以忽略.所以,如果是尺寸很大的体系,我们可以不管两者的区别而只采用周期边界的形式,并且设动量取在第一布里渊区,即 k\in[-\pi,\pi] .
代入傅里叶变换可得体系的哈密顿量在动量空间可以化为
\begin{eqnarray} \hat{H}_{XY}=\sum_{k}(-J\cos k)\hat{f}_{k}^{\dag}\hat{f}_{k} \end{eqnarray}
在零温基态,费米子根据色散 -J\cos k<0 填满 k\in[-\frac{\pi}{2},\frac{\pi}{2}] 的半个一维第一布里渊区,基态波函数用费米子可以表示为
\begin{equation} |\Psi_{g}\rangle=\prod_{k<k_{F}}\hat{f}_{k}^{\dag}|0,0,0...\rangle,~k_{F}=\pi/2. \end{equation}
此时必然有 \langle \hat{f}_{k}^{\dag}\hat{f}_{k}\rangle_{T=0}=\theta(\frac{\pi}{2}-|k|) ,这样z方向的磁化是
\begin{equation} \langle\hat{S}_{j}^{z}\rangle_{T=0}=\langle\hat{f}_{j}^{\dag}\hat{f}_{j}\rangle_{T=0}-\frac{1}{2}= \frac{1}{N_{s}}\sum_{k}\langle\hat{f}_{k}^{\dag}\hat{f}_{k}\rangle_{T=0}-\frac{1}{2}= \int_{-\pi}^{\pi}\frac{dk}{2\pi}\theta\left(\frac{\pi}{2}-|k|\right)-\frac{1}{2}=0 \end{equation}
换句话说,基态时的一维量子XY模型磁化为零,处于无序态.虽然用费米子表示的基态波函数已经写出,但如果转换至原始的自旋语言却比较复杂,
\begin{eqnarray} |\Psi_{g}\rangle&=&\prod_{k<k_{F}}\frac{1}{\sqrt{N_{s}}}\sum_{j}e^{-ikR_{j}}\hat{f}_{j}^{\dag}|0,0,0...\rangle\nonumber\\ &=&\prod_{k<k_{F}}\frac{1}{\sqrt{N_{s}}}\sum_{j}e^{-ikR_{j}}\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}|\downarrow,\downarrow,\downarrow...\rangle. \end{eqnarray}
例如,考虑 N_{s}=4 ,那么动量取值为 k=\frac{2\pi}{4}n(n=\pm\frac{1}{2},\pm\frac{3}{2}) . [5] 既然费米波矢 k_{F}=\pi/2 ,那么基态时候占据的动量就是 k=\pm\frac{\pi}{4} .我们发现此时的基态波函数是
\begin{eqnarray} |\Psi_{g}\rangle &=&\frac{1}{\sqrt{4}}\sum_{j=1}^{4}e^{-i\frac{\pi}{4}R_{j}}\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}\frac{1}{\sqrt{4}}\sum_{j'=1}^{4}e^{i\frac{\pi}{4}R_{j'}}\hat{S}_{j'}^{+}e^{i\pi\sum_{m'<j'}(\hat{S}_{m'}^{z}+1/2)}|\downarrow,\downarrow,\downarrow,\downarrow\rangle\nonumber\\ &=&\frac{1}{4} (e^{-i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{-i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)}+ e^{-i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)}+ e^{-i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)})\nonumber\\ &\times&(e^{i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)} +e^{i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)} +e^{i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)}) |\downarrow,\downarrow,\downarrow,\downarrow\rangle\nonumber\\ &=&\frac{1}{4} (e^{-i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{-i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)}+ e^{-i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)}+ e^{-i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)})\nonumber\\ &\times&(e^{i\frac{\pi}{4}}|\uparrow,\downarrow,\downarrow,\downarrow\rangle +e^{i\frac{\pi}{4}2}|\downarrow,\uparrow,\downarrow,\downarrow\rangle +e^{i\frac{\pi}{4}3}|\downarrow,\downarrow,\uparrow,\downarrow\rangle +e^{i\frac{\pi}{4}4}|\downarrow,\downarrow,\downarrow,\uparrow\rangle). \end{eqnarray}
完成上述计算可以看到 |\Psi_{g}\rangle 包含6项:
\begin{eqnarray} |\Psi_{g}\rangle &=&\frac{i}{2}\sin\frac{\pi}{4}(|\uparrow,\uparrow,\downarrow,\downarrow\rangle+|\downarrow,\uparrow,\uparrow,\downarrow\rangle)\nonumber\\ &+&\frac{i}{2}\sin\frac{2\pi}{4}(|\downarrow,\uparrow,\downarrow,\uparrow\rangle+|\uparrow,\downarrow,\downarrow,\uparrow\rangle)\nonumber\\ &+&\frac{i}{2}\sin\frac{3\pi}{4}(|\uparrow,\downarrow,\uparrow,\downarrow\rangle+|\downarrow,\downarrow,\uparrow,\uparrow\rangle)\nonumber. \end{eqnarray}
这种不同自旋构型之间的高度混合是零温磁性无序态的典型特征,用现代的语言来说就是所谓的量子自旋液体态.
为了便于参考,体系的基态能密度是
\begin{equation} \frac{E_{g}}{N_{s}}=\frac{1}{N_{s}}\sum_{k}-J\cos k\theta(J\cos k)=\int_{-\pi/2}^{\pi/2}\frac{dk}{2\pi}(-J\cos k)=-\frac{J}{\pi}. \end{equation}
高维Jordan-Wigner变换的困难
在结束这一小节的讨论前,让我们感受一下一维Jordan-Wigner变换直接推广到高维的困难.为简单起见,我们考虑两个耦合的XY模型所组成的自旋双链,这可以看作是二维系统的一维极限,
\begin{equation} \hat{H}=-\frac{J_{1}}{2}\sum_{j}[\hat{S}_{aj}^{+}\hat{S}_{aj+1}^{-}+\hat{S}_{aj}^{-}\hat{S}_{aj+1}^{+}] -\frac{J_{2}}{2}\sum_{j}[\hat{S}_{bj}^{+}\hat{S}_{bj+1}^{-}+\hat{S}_{bj}^{-}\hat{S}_{bj+1}^{+}]-\frac{w}{2}\sum_{j}[\hat{S}_{aj}^{+}\hat{S}_{bj}^{-}+\hat{S}_{aj}^{-}\hat{S}_{bj}^{+}] \end{equation}
这里指标 a,b 分别代表第一和第二个XY自旋链, J_{1},J_{2} 是链内的XY耦合,w是链间耦合.仿照一维XY模型的处理,我们可以假象把第二条自旋链直接拼接到第一条链的末端而形成等效的一维链,这样就可以套用Jordan-Wigner变换的基本形式,即有:
\begin{eqnarray} &&\hat{S}_{aj}^{+}=\hat{f}_{aj}^{\dag}e^{i\hat{\phi}_{aj}},~~\hat{\phi}_{aj}=\pi\sum_{1\leq m<j}\hat{f}_{am}^{\dag}\hat{f}_{am},~~\hat{S}_{aj}^{z}=\hat{f}_{aj}^{\dag}\hat{f}_{aj}-\frac{1}{2}\nonumber\\ &&\hat{S}_{bj}^{+}=\hat{f}_{bj}^{\dag}e^{i\hat{\phi}_{bj}},~~\hat{\phi}_{bj}=\pi\sum_{m}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm},~~\hat{S}_{bj}^{z}=\hat{f}_{bj}^{\dag}\hat{f}_{bj}-\frac{1}{2}\nonumber \end{eqnarray}
注意到第二个自旋链的每个相位因子 \hat{\phi}_{bj} 感受同一个自旋链上自旋的影响还会受到第一个自旋链的影响,即 \pi\sum_{m}\hat{f}_{am}^{\dag}\hat{f}_{am} .把这个变换代入模型可得
\begin{eqnarray} \hat{H}&=&-\frac{J_{1}}{2}\sum_{j}[\hat{f}_{aj}^{\dag}\hat{f}_{aj+1}+h.c.] -\frac{J_{2}}{2}\sum_{j}[\hat{f}_{bj}^{\dag}\hat{f}_{bj+1}+h.c.]\nonumber\\ &-&\frac{w}{2}\sum_{j}[\hat{f}_{aj}^{\dag}e^{i(\pi\sum_{m\geq j}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm})}\hat{f}_{bj}+h.c.] \end{eqnarray}
我们发现描述自旋链耦合的 w 项出现了难以处理的费米子算符的指数形式 e^{i(\pi\sum_{m\geq j}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm})} ,这是从a自旋链上j格点到b自旋链j格点的Jordan-Wigner弦.显然,一般的二维自旋模型可以看作很多不同的一维自旋链的耦合,由于不同链间Jordan-Wigner弦的存在,自旋模型无法变换为简单的自由费米子问题而成为相互作用费米子问题,这就是Jordan-Wigner变换直接高维推广所面临的基本困难.
参考
- ^ U(1)/O(2)表明自旋绕着z轴转动不变
- ^ 定义一个量子力学问题需要定义Hilbert空间以及算符
- ^ Jordan,Wigner,About the Pauli exclusion principle,Z.Phys. 47,631(1928)这文章是用德文写的,看不懂!
- ^ 一般会包换规范场类型的自由度以及费米子自由度
- ^ 这里是费米子取反周期边界










