这一part讲著名的Jordan–Wigner变换,知乎上已经有许多类似的帖子可参考。
顺便也拿来当个回答
非相互作用的费米子气体依然是高度关联的,像不相容原理引入了同一个量子态的费米子之间的硬核相互作用,而Jordan–Wigner变换即利用该相互作用来表征自旋。
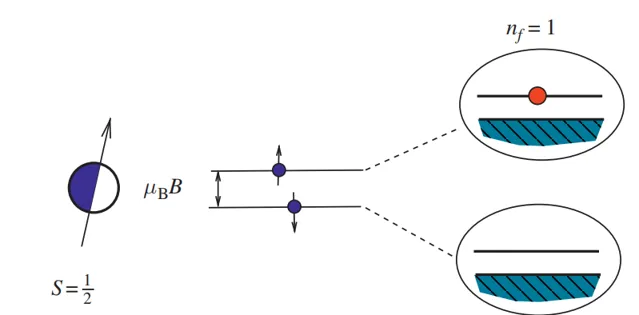
在多体物理中,自旋不像费米子or玻色子那样好处理,不过在一维的体系中,自旋 S=1/2 具有和费米子类似的特征。Jordan和Wigner这俩哥们注意到单自旋的「上」和「下」可以被认为是费米子的空态与占据态。因此可以做mapping(如下图):
|\uparrow\rangle=f^\dag |0\rangle,\ |\downarrow\rangle=|0\rangle (3.1)
用矩阵表示自旋上升和下降算符即为:
\begin{aligned} &S^+=f^\dag=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \\ &S^-=f=\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \end{aligned} (3.2)
自旋算符的z分量可以写为:
S_z=\frac{1}{2}\left[ |\uparrow\rangle\langle\uparrow|-|\downarrow\rangle\langle\downarrow| \right]=f^\dag f-\frac{1}{2} (3.3)
当然我们也能重写其它的自旋算符:
\begin{aligned} &S_x=\frac{1}{2}(S^++S^-)=\frac{1}{2}(f^\dag+f) \\ &S_y=\frac{1}{2i}(S^+-S^-)=\frac{1}{2i}(f^\dag-f) \end{aligned} (3.4)
当然这些矩阵形式也满足以下代数:
\left[ S_a,S_b \right]=i\epsilon_{abc}S_c (3.5)
由于隐藏的对称性,它们也满足反对易关系:
\left\{ S_a,S_b \right\}=\frac{1}{4}\left\{ \sigma_a,\sigma_b \right\}=\frac{1}{2}\delta_{ab} (3.6)
则泡利算符为Jordan and Wigner提供了个费米子的基本模型。但如果有多个自旋,因为自旋和费米子的对易关系不一致,咱得做一些小小的修改,他俩人就发现在费米子上加一个相位因子就能搞定这个问题。
对于一个一维的自旋链,在格点 j 的自旋算符可以表示为:
S^+_j=f^\dag_j e^{i\phi_j} (3.7)
其中相位因子 e^{i\phi_j} 包含了格点 j 左边所有费米子占据量的总和:
\phi_j=\pi\underset{l<j}{\sum}n_l (3.8)
该 e^{i\hat{\phi}_j} 即为弦算符。我们可以得到完整ordan-Wigner变换:
\begin{aligned} &S^z_j=f^\dag_jf_j-\frac{1}{2} \\ &S^+_j=f^\dag_je^{i\pi\sum_{l<j}n_l} \\ &S^-_j=f_je^{-i\pi\sum_{l<j}n_l} \end{aligned} (3.9)
注意 e^{i\pi n_j}=e^{-i\pi n_j} 是厄密的,so相位因子的负号也是能被反转的同时还不改变自旋算符。用图片表示改变换的话:

即为:自旋=费米子×弦。
弦有个重要性质,它和任意在其左边的费米子算符反对易。由于 f_j 会减少个 n_j ,让粒子数从1变到0,因此当 e^{i\pi n_j} 作用到 |1\rangle 时为例,可以得到 n_j=1,e^{i\pi n_j}=-1 ,代入此时的 f_je^{i\pi n_j}|1\rangle 得到 -f_j|1\rangle=-|0\rangle ;相反我们先作用一个 f_j 再作用 e^{i\pi n_j} 得到的 n_j=0,e^{i\pi n_j}=1 ,则 e^{i\pi n_j}f_j|1\rangle=|0\rangle ,则有
\left\{ e^{i\pi n_j},f_j \right\}=e^{i\pi n_j}f_j+fe^{i\pi n_j}=0 (3.10)
这里原文用的是其它讲法,我是以 |1\rangle 为例可能更易懂一点
之后咱可以用相似的方法得到 \left\{ e^{i\pi n_j},f^\dag_j \right\}=0 。现在这个相位因子 e^{i\pi n_l} 在其它格点 l\ne j 都和 f_j 、 f^\dag_j 对易,则弦算符 e^{i\phi_j} 和所有 j 左边的费米子算符反对易,即
\left\{ e^{i\phi_j},f^{(\dag)}_l \right\}=0 \ (l<j)
却会和其它格点的费米子对易
\left[ e^{i\phi_j},f^{(\dag)}_l \right]=0\ (l\geq j)
OK我们现在可以确认一些与自旋算符对应的对易关系,其中 j<k 且 e^{i\phi_j} 和格点 j 、 k 的费米子对易,有:
[S^{(\pm)}_j,S^{(\pm)}_k]=[f^{(\dag)}_je^{i\phi_j} , f^{\dag}_k e^{i\phi_k}]=e^{i\phi_j} [f^{(\dag)},f^{(\dag)}e^{i\phi_k}]
但和、都反对易,so它和它们俩的乘积对易,因此有
[S^{(\pm)}_j,S^{(\pm)}_k]\propto[f^{(\dag)}_j,f^{(\dag)}_k e^{i\phi_k}]=0 (3.11)
有趣的是通过给费米子加上弦算符,它们可以转换成玻色子。
From Introduction to Many-Body PhysicsIntroduction to Many-Body Physics of Piers Coleman










