Serre对偶定理:复流形上的全纯向量丛与上同调群
Serre对偶定理是复几何和代数几何中的一个核心概念,它建立了紧致复流形上全纯向量丛的上同调群之间的深刻联系。这一定理不仅为我们提供了一种计算全纯向量丛的上同调群的有效方法,还揭示了复流形上几何结构与代数性质之间的微妙关系。
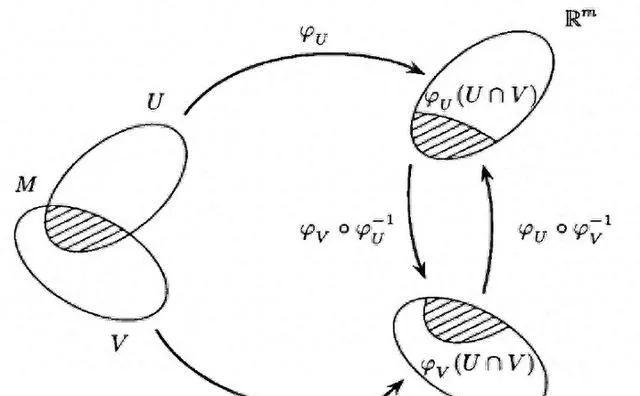
紧致复流形与全纯向量丛
紧致复流形是复分析中的一类重要对象,它们是在复数域上定义的、具有紧致拓扑结构的流形。全纯向量丛则是流形上的一种几何结构,它为流形的每一点都赋予了一个复数向量空间,并且这些向量空间在流形上平滑地变化。
Serre对偶定理的陈述
根据Serre对偶定理,对于紧致复流形X上的任意整数k和两个全纯向量丛E、F,存在一个自然的同构:
H^k(X, E ⊗ Ω^n_X) ≅ H^{n-k}(X, E^* ⊗ F)
其中,H^k(X, E ⊗ Ω^n_X)表示X上关于E与X的全纯n-形式丛Ω^n_X的张量积的上k阶Dolbeault上同调群;E*是E的对偶丛;Ω^n_X是X上的全纯n-形式丛,即X上所有全纯n-形式的集合;⊗表示向量丛的张量积。
定理的几何意义

Serre对偶定理的几何意义在于它揭示了复流形上全纯向量丛的上同调群之间的对偶关系。这种对偶关系在数学和物理学中都扮演着重要角色,尤其是在弦论和量子场论中,它为我们提供了一种理解和描述复杂系统的新视角。
定理的应用
Serre对偶定理在复几何和代数几何中有着广泛的应用。例如,在代数几何中,我们可以利用该定理研究代数曲线和代数曲面上的全纯向量丛的性质,从而得到关于这些曲线和曲面的重要信息。此外,该定理还可以用于计算全纯向量丛的上同调群,这对于理解复流形的几何结构和拓扑性质具有重要意义。
结论
总的来说,Serre对偶定理是复几何和代数几何中的一个基本而重要的定理。它不仅为我们提供了一种计算全纯向量丛的上同调群的有效方法,还揭示了复流形上几何结构与代数性质之间的深刻联系。通过深入研究和应用这一定理,我们可以更好地理解和描述复流形及其上的全纯向量丛的几何结构和拓扑性质,从而为数学和物理学中的其他领域提供有力支持。











