這一part講著名的Jordan–Wigner變換,知乎上已經有許多類似的貼文可參考。
順便也拿來當個回答
非交互作用的費米子瓦斯依然是高度關聯的,像不相容原理引入了同一個量子態的費米子之間的硬核交互作用,而Jordan–Wigner變換即利用該交互作用來表征自旋。
在多體物理中,自旋不像費米子or玻色子那樣好處理,不過在一維的體系中,自旋 S=1/2 具有和費米子類別似的特征。Jordan和Wigner這倆哥們註意到單自旋的「上」和「下」可以被認為是費米子的空態與占據態。因此可以做mapping(如下圖):
|\uparrow\rangle=f^\dag |0\rangle,\ |\downarrow\rangle=|0\rangle (3.1)
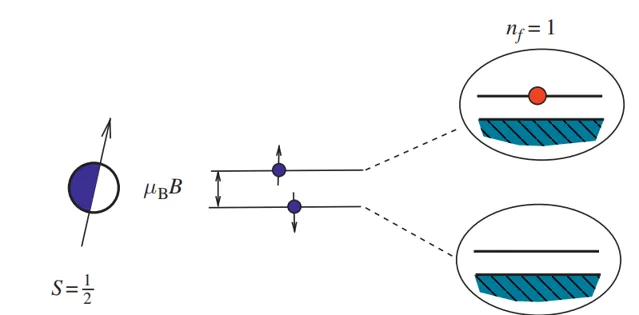
用矩陣表示自旋上升和下降算符即為:
\begin{aligned} &S^+=f^\dag=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \\ &S^-=f=\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \end{aligned} (3.2)
自旋算符的z分量可以寫為:
S_z=\frac{1}{2}\left[ |\uparrow\rangle\langle\uparrow|-|\downarrow\rangle\langle\downarrow| \right]=f^\dag f-\frac{1}{2} (3.3)
當然我們也能重寫其它的自旋算符:
\begin{aligned} &S_x=\frac{1}{2}(S^++S^-)=\frac{1}{2}(f^\dag+f) \\ &S_y=\frac{1}{2i}(S^+-S^-)=\frac{1}{2i}(f^\dag-f) \end{aligned} (3.4)
當然這些矩陣形式也滿足以下代數:
\left[ S_a,S_b \right]=i\epsilon_{abc}S_c (3.5)
由於隱藏的對稱性,它們也滿足反對易關系:
\left\{ S_a,S_b \right\}=\frac{1}{4}\left\{ \sigma_a,\sigma_b \right\}=\frac{1}{2}\delta_{ab} (3.6)
則包立算符為Jordan and Wigner提供了個費米子的基本模型。但如果有多個自旋,因為自旋和費米子的對易關系不一致,咱得做一些小小的修改,他倆人就發現在費米子上加一個相位因子就能搞定這個問題。
對於一個一維的自旋鏈,在格點 j 的自旋算符可以表示為:
S^+_j=f^\dag_j e^{i\phi_j} (3.7)
其中相位因子 e^{i\phi_j} 包含了格點 j 左邊所有費米子占據量的總和:
\phi_j=\pi\underset{l<j}{\sum}n_l (3.8)
該 e^{i\hat{\phi}_j} 即為弦算符。我們可以得到完整ordan-Wigner變換:
\begin{aligned} &S^z_j=f^\dag_jf_j-\frac{1}{2} \\ &S^+_j=f^\dag_je^{i\pi\sum_{l<j}n_l} \\ &S^-_j=f_je^{-i\pi\sum_{l<j}n_l} \end{aligned} (3.9)
註意 e^{i\pi n_j}=e^{-i\pi n_j} 是厄密的,so相位因子的負號也是能被反轉的同時還不改變自旋算符。用圖片表示改變換的話:
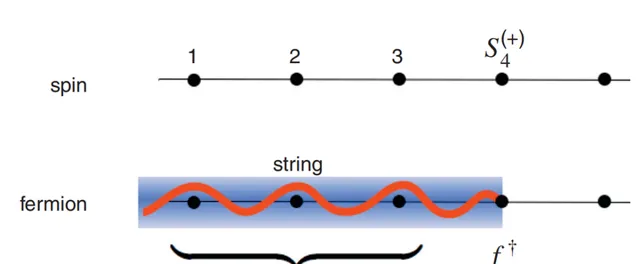
即為:自旋=費米子×弦。
弦有個重要性質,它和任意在其左邊的費米子算符反對易。由於 f_j 會減少個 n_j ,讓粒子數從1變到0,因此當 e^{i\pi n_j} 作用到 |1\rangle 時為例,可以得到 n_j=1,e^{i\pi n_j}=-1 ,代入此時的 f_je^{i\pi n_j}|1\rangle 得到 -f_j|1\rangle=-|0\rangle ;相反我們先作用一個 f_j 再作用 e^{i\pi n_j} 得到的 n_j=0,e^{i\pi n_j}=1 ,則 e^{i\pi n_j}f_j|1\rangle=|0\rangle ,則有
\left\{ e^{i\pi n_j},f_j \right\}=e^{i\pi n_j}f_j+fe^{i\pi n_j}=0 (3.10)
這裏原文用的是其它講法,我是以 |1\rangle 為例可能更易懂一點
之後咱可以用相似的方法得到 \left\{ e^{i\pi n_j},f^\dag_j \right\}=0 。現在這個相位因子 e^{i\pi n_l} 在其它格點 l\ne j 都和 f_j 、 f^\dag_j 對易,則弦算符 e^{i\phi_j} 和所有 j 左邊的費米子算符反對易,即
\left\{ e^{i\phi_j},f^{(\dag)}_l \right\}=0 \ (l<j)
卻會和其它格點的費米子對易
\left[ e^{i\phi_j},f^{(\dag)}_l \right]=0\ (l\geq j)
OK我們現在可以確認一些與自旋算符對應的對易關系,其中 j<k 且 e^{i\phi_j} 和格點 j 、 k 的費米子對易,有:
[S^{(\pm)}_j,S^{(\pm)}_k]=[f^{(\dag)}_je^{i\phi_j} , f^{\dag}_k e^{i\phi_k}]=e^{i\phi_j} [f^{(\dag)},f^{(\dag)}e^{i\phi_k}]
但和、都反對易,so它和它們倆的乘積對易,因此有
[S^{(\pm)}_j,S^{(\pm)}_k]\propto[f^{(\dag)}_j,f^{(\dag)}_k e^{i\phi_k}]=0 (3.11)
有趣的是透過給費米子加上弦算符,它們可以轉換成玻色子。
From Introduction to Many-Body PhysicsIntroduction to Many-Body Physics of Piers Coleman










