一維量子XY模型與Jordan-Wigner變換
Jordan-Wigner變換是求解某些一維量子自旋模型的有力方法,它對於我們理解一維自旋系統的一般特征是很有價值的。當然,除了一維自旋體系,部份二維自旋系統也可以用Jordan-Wigner變換求解,例如著名的Kitaev honeycomb模型,關於其求解在我們先前的文章中已經介紹,感興趣的讀者可以參考:
讓我們考慮一維量子XY模型,其描述x與y方向的自旋交換耦合.
\begin{equation} \hat{H}_{XY}=-J\sum_{j}[\hat{S}_{j}^{x}\hat{S}_{j+1}^{x}+\hat{S}_{j}^{y}\hat{S}_{j+1}^{y}]=-\frac{J}{2}\sum_{j}[\hat{S}_{j}^{+}\hat{S}_{j+1}^{-}+\hat{S}_{j}^{-}\hat{S}_{j+1}^{+}] \end{equation}
這裏的自旋 1/2 算符滿足 SU(2) 對易關系 [\hat{S}_{j}^{\alpha},\hat{S}_{k}^{\beta}]=i\varepsilon^{\alpha\beta\gamma}\delta_{jk}\hat{S}_{k}^{\gamma} . 註意到與具有完全自旋 SU(2) 旋轉對稱的Heisenberg模型相比,這裏少了 z 方向的耦合
\begin{equation} -J\sum_{j}\hat{S}_{j}^{z}\hat{S}_{j+1}^{z} \end{equation}
換句話說,體系的對稱性從 SU(2) 減少到 U(1) 或 O(2) . [1]
單個S=1/2自旋的費米子表示
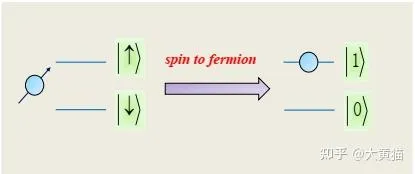
對於一個孤立的S=1/2自旋,其Hilbert空間與一個無自旋費米子是相似的,這提示我們自旋與費米子之間可能有如下對應關系:
\begin{equation} |\downarrow\rangle\leftrightarrow |0\rangle,~~|\uparrow\rangle\leftrightarrow |1\rangle=\hat{f}^{\dag}|0\rangle \end{equation}
也就是說我們可以把自旋的下態對應沒有費米子的狀態,而自旋上態對應有一個費米子的狀態.那麽相應的算符也有如下的對應 [2]
\begin{equation} \hat{S}^{+}=\hat{f}^{\dag},~~\hat{S}^{-}=\hat{f},~~\hat{S}^{z}=\hat{f}^{\dag}\hat{f}-\frac{1}{2}. \end{equation}
讓我們檢驗自旋算符間的對易或反對易關系是否能夠由上述費米子表示來實作.首先,我們知道,對於S=1/2自旋有 (\hat{S}^{x})^{2}=(\hat{S}^{y})^{2}=(\hat{S}^{z})^{2}=\frac{1}{4} 或者說 \hat{\vec{S}}\cdot\hat{\vec{S}}=\frac{3}{4}.而由\hat{S}^{\pm}=\hat{S}^{x}\pm i\hat{S}^{y} 可得
\begin{equation} \hat{S}^{x}=\frac{1}{2}(\hat{S}^{+}+\hat{S}^{-})=\frac{1}{2}(\hat{f}^{\dag}+\hat{f}), ~\hat{S}^{y}=\frac{1}{2i}(\hat{S}^{+}-\hat{S}^{-})=\frac{1}{2i}(\hat{f}^{\dag}-\hat{f}). \end{equation}
這樣就有
\begin{equation} (\hat{S}^{x})^{2}=\frac{1}{4}(\hat{f}^{\dag}+\hat{f})(\hat{f}^{\dag}+\hat{f})=\frac{1}{4}\{\hat{f}^{\dag},\hat{f}\}=\frac{1}{4}. \end{equation}
註意到我們(將會)大量使用費米子算符自乘為零這一性質,即 \hat{f}^{\dag}\hat{f}^{\dag}=\hat{f}\hat{f}=0 以及費米子的反對易關系 \{\hat{f}^{\dag},\hat{f}\}=\hat{f}\hat{f}^{\dag}+\hat{f}^{\dag}\hat{f}=1 .類似的,我們發現 (\hat{S}^{y})^{2}=\frac{1}{4i^{2}}(-1)\{\hat{f}^{\dag},\hat{f}\}=\frac{1}{4} ,
\begin{equation} (\hat{S}^{z})^{2}=\left(\hat{f}^{\dag}\hat{f}-\frac{1}{2}\right)\left(\hat{f}^{\dag}\hat{f}-\frac{1}{2}\right) =\overbrace{\hat{f}^{\dag}\hat{f}\hat{f}^{\dag}\hat{f}}^{=\hat{f}^{\dag}\hat{f}}-\hat{f}^{\dag}\hat{f}+\frac{1}{4}=\frac{1}{4}. \end{equation}
因此,自旋算符平方為 1/4 確實可用費米子完全表示.接下來, \hat{S}^{x},\hat{S}^{y} 的對易關系是
\begin{eqnarray} [\hat{S}^{x},\hat{S}^{y}]=\frac{1}{4i}[\hat{f}^{\dag}+\hat{f},\hat{f}^{\dag}-\hat{f}]=\frac{1}{2i}(1-2\hat{f}^{\dag}\hat{f})=i\hat{S}^{z}. \end{eqnarray}
\hat{S}^{y},\hat{S}^{z} 的對易關系是
\begin{eqnarray} [\hat{S}^{y},\hat{S}^{z}]=\frac{1}{2i}[\hat{f}^{\dag}-\hat{f},\hat{f}^{\dag}\hat{f}]=-\frac{1}{2i}(\hat{f}\hat{f}^{\dag}\hat{f}+\hat{f}^{\dag}\hat{f}\hat{f}^{\dag}) =-\frac{1}{2i}(\hat{f}+\hat{f}^{\dag})=i\hat{S}^{x}.\nonumber \end{eqnarray}
顯然,費米子表示也可以得到正確的自旋對易關系.最後,讓我們自旋間的反對以關系也可用費米子成功表示,即
\begin{equation} \{\hat{S}^{x},\hat{S}^{y}\}=\frac{1}{4i}\{\hat{f}^{\dag}+\hat{f},\hat{f}^{\dag}-\hat{f}\}=0. \end{equation}
\begin{equation} \{\hat{S}^{y},\hat{S}^{z}\}=\frac{1}{2i}\{\hat{f}^{\dag}-\hat{f},\hat{f}^{\dag}\hat{f}-1/2\}= \frac{1}{2i}(-\hat{f}-\hat{f}^{\dag}+\hat{f}\hat{f}^{\dag}\hat{f}+\hat{f}^{\dag}\hat{f}\hat{f}^{\dag})= \frac{1}{2i}(-\hat{f}-\hat{f}^{\dag}+\hat{f}+\hat{f}^{\dag})=0. \end{equation}
兩個S=1/2自旋的費米子表示
在用費米子成功表示單個S=1/2自旋後,讓我們考慮多個自旋的情況,例如兩個自旋, \hat{\vec{S}}_{1},\hat{\vec{S}}_{2} .我們知道,不同自旋之間是互相對易的,如果直接套用單個自旋的費米子表示,(j=1,2)
\begin{equation} \hat{S}^{x}_{j}=\frac{1}{2}(\hat{f}^{\dag}_{j}+\hat{f}_{j}), ~\hat{S}^{y}_{j}=\frac{1}{2i}(\hat{f}^{\dag}_{j}-\hat{f}_{j}),~\hat{S}^{z}_{j}=\hat{f}^{\dag}_{j}\hat{f}_{j}-\frac{1}{2} \end{equation}
那麽會發現,
\begin{eqnarray} [\hat{S}^{x}_{1},\hat{S}^{y}_{2}]&=&\frac{1}{4i}[\hat{f}^{\dag}_{1}+\hat{f}_{1},\hat{f}^{\dag}_{2}-\hat{f}_{2}]\nonumber\\ &=&\frac{1}{4i}[\overbrace{(\hat{f}^{\dag}_{1}\hat{f}^{\dag}_{2}-\hat{f}^{\dag}_{1}\hat{f}_{2}+\hat{f}_{1}\hat{f}^{\dag}_{2}-\hat{f}_{1}\hat{f}_{2})}^{\hat{W}_{12}}- (\overbrace{\hat{f}^{\dag}_{2}\hat{f}^{\dag}_{1}-\hat{f}^{\dag}_{2}\hat{f}_{1}+\hat{f}_{2}\hat{f}^{\dag}_{1}-\hat{f}_{2}\hat{f}_{1})}^{\hat{W}_{21}}]\neq0.\nonumber \end{eqnarray}
可以看到,上式中 \hat{W}_{12},\hat{W}_{21}(\hat{W}_{12}=-\hat{W}_{21}) 因為對易關系本身的負號而無法抵消.這說明簡單的推廣單個自旋的費米子表示不能正確反映不同自旋間的對易關系.註意到如果因為某種原因,我們可以給 \hat{W}_{21} 前面再添加上一個負號,那麽 \hat{W}_{12}+(-1)^{2}\hat{W}_{21}=0 .所以,我們需要尋找一種方案,使得不同自旋之間做對易關系時出現一個負號,歷史上,這個關系由Jordan和Wigner發現,即所謂的Jordan-Wigner變換. [3]
Jordan-Wigner變換
考慮定義在晶格格點上的自旋,由於每個格點間的自旋是對易的(每個格點的自旋是可分辨的),因此我們需要額外的東西來確保不同格點自旋的對易性.註意到費米子之間反對易,因此需要添加的可以是一個產生額外負號的相位因子部份,對一維自旋系統而言,Jordan-Wigner變換明確給出S=1/2系統與費米子系統的對應:
\begin{eqnarray} \boxed{\hat{S}_{j}^{+}=\hat{f}_{j}^{\dag}e^{i\hat{\phi}_{j}},~~\hat{\phi}_{j}=\pi\sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m},~~\hat{S}_{j}^{z}=\hat{f}_{j}^{\dag}\hat{f}_{j}-\frac{1}{2}} \end{eqnarray}
這裏 \hat{S}_{j}^{+},\hat{S}_{j}^{z} 是第 j 個(格點)的 S=1/2 自旋算符,滿足標準的對易關系 [\hat{S}_{j}^{x},\hat{S}_{k}^{y}]=i\delta_{j,k}\hat{S}_{j}^{z}.\hat{f}^{\dag}_{j},\hat{f}_{j} 是標準的費米子算符,滿足反對易關系 \{\hat{f}_{j},\hat{f}_{k}^{\dag}\}=\delta_{j,k} .相因子部份 e^{i\hat{\phi}_{j}}=e^{i\pi\sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m}}=e^{i\pi\sum_{1\leq m<j}(\hat{S}_{m}^{z}+1/2)} 稱為Jordan-Wigner弦(算符),其與 \hat{f}_{j}^{\dag},\hat{f}_{j} 都是對易的.Jordan-Wigner弦物理意義是 j 格點的自旋算符感受到其他自旋對其的相位調變.
在一維鏈的情況下, j 格點的相位 \phi_{j} 依賴於第一個到 j-1 格點的費米子的占據數 \sum_{1\leq m<j}\hat{f}_{m}^{\dag}\hat{f}_{m} ,每存在一個費米子就會貢獻一個相位 \pi ,總的相位便是所有 j 格點左側格點的相位之和.
在實際使用中,我們註意到
\begin{equation} e^{i\pi\hat{f}_{m}^{\dag}\hat{f}_{m}}=(-1)^{\hat{f}_{m}^{\dag}\hat{f}_{m}}=1-2\hat{f}_{m}^{\dag}\hat{f}_{m} \end{equation}
比較上式兩邊的本征值就可證明這個關系.另外,
\begin{equation} \hat{S}_{j}^{-}=\hat{f}_{j}e^{-i\hat{\phi}_{j}}=\hat{f}_{j}e^{i\hat{\phi}_{j}}. \end{equation}
也就是說 e^{-i\hat{\phi}_{j}}=e^{i\hat{\phi}_{j}} .這樣 e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{j}}=e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}=1 .
\begin{equation} \hat{S}_{j}^{x}=\frac{1}{2}(\hat{S}_{j}^{+}+\hat{S}_{j}^{-})=\frac{1}{2}(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}. \end{equation}
\begin{equation} \hat{S}_{j}^{y}=\frac{1}{2i}(\hat{S}_{j}^{+}-\hat{S}_{j}^{-})=\frac{1}{2i}(\hat{f}_{j}^{\dag}-\hat{f}_{j})e^{i\hat{\phi}_{j}}. \end{equation}
反過來,我們也可以用自旋來表示費米子,即有
\begin{equation} \hat{f}_{j}^{\dag}=\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}=\hat{S}_{j}^{+}\prod_{m<j}\hat{R}_{m}(\vec{e}_{z},\pi)e^{i\pi(j-1)/2} \end{equation}
註意到自旋旋轉算符 \hat{R}_{m}(\vec{e}_{z},\pi) 會使得 \hat{S}_{m}^{x}\rightarrow-\hat{S}_{m}^{x},\hat{S}_{m}^{y}\rightarrow-\hat{S}_{m}^{y} ,這樣當費米子算符 \hat{f}_{j}^{\dag} 作用於 |\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow\rightarrow...\rangle 得到 |\leftarrow\leftarrow\leftarrow\rightarrow\rightarrow\rightarrow...\rangle ,也就是相對於自旋取向均為 S^{x}=1/2 的態產生一個在 j 處的疇壁.這說明費米子算符就是疇壁的產生或者湮滅算符,即XY模型中的疇壁是費米子.
為了討論的完整性,讓我們驗證自旋算符滿足想要的對易關系.對於同一個格點的自旋,Jordan-Wigner弦算符互相抵消,因此其對易關系與單個 S=1/2 自旋是一致的.對於不同格點自旋,例如 \hat{S}_{j}^{x},\hat{S}_{k}^{y} (設 j<k )的對易關系:
\begin{eqnarray} [\hat{S}^{x}_{j},\hat{S}^{y}_{k}]&=&\frac{1}{4i}[(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}},(\hat{f}_{k}^{\dag}-\hat{f}_{k})e^{i\hat{\phi}_{k}}]\nonumber\\ &=&\frac{1}{4i}\left((\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}(\hat{f}_{k}^{\dag}-\hat{f}_{k}) -(\hat{f}_{k}^{\dag}-\hat{f}_{k})e^{i\hat{\phi}_{k}}e^{i\hat{\phi}_{j}}(\hat{f}_{j}^{\dag}+\hat{f}_{j})\right).\nonumber \end{eqnarray}
註意到
\begin{equation} e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}=e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}e^{i\pi \hat{f}_{j}^{\dag}f_{j}}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(1-2\hat{f}_{j}^{\dag}f_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}. \end{equation}
那麽
\begin{eqnarray} (\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\hat{\phi}_{j}}e^{i\hat{\phi}_{k}}= (\hat{f}_{j}^{\dag}+\hat{f}_{j})(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(\hat{f}_{j}^{\dag}-\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}.\nonumber \end{eqnarray}
另一方面,
\begin{eqnarray} e^{i\hat{\phi}_{k}}e^{i\hat{\phi}_{j}}(\hat{f}_{j}^{\dag}+\hat{f}_{j}) =(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})(\hat{f}_{j}^{\dag}+\hat{f}_{j})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}=(\hat{f}_{j}-\hat{f}_{j}^{\dag})e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}.\nonumber \end{eqnarray}
所以
\begin{eqnarray} [\hat{S}^{x}_{j},\hat{S}^{y}_{k}]&=&\frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}\left((\hat{f}_{j}^{\dag}-\hat{f}_{j})(\hat{f}_{k}^{\dag}-\hat{f}_{k}) -(\hat{f}_{k}^{\dag}-\hat{f}_{k})(\hat{f}_{j}-\hat{f}_{j}^{\dag})\right)\nonumber\\ &=& \frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}}\left((\hat{f}_{j}^{\dag}-\hat{f}_{j})(\hat{f}_{k}^{\dag}-\hat{f}_{k}) +(-1)^{2}(\hat{f}_{k}^{\dag}-\hat{f}_{k})(\hat{f}_{j}^{\dag}-\hat{f}_{j})\right)\nonumber\\ &=&\frac{1}{4i}e^{i\pi \sum_{j<m<k}\hat{f}_{m}^{\dag}f_{m}} \left( \{\hat{f}_{j}^{\dag},\hat{f}_{k}^{\dag}\} -\{\hat{f}_{j}^{\dag},\hat{f}_{k}\} -\{\hat{f}_{j},\hat{f}_{k}^{\dag}\} +\{\hat{f}_{j},\hat{f}_{k}\}\right)=0.\nonumber \end{eqnarray}
最後,容易發現,
\begin{equation} [\hat{S}_{j}^{y},\hat{S}_{k}^{z}]=\frac{1}{2i}e^{i\hat{\phi}_{j}}[\hat{f}^{\dag}_{j}-\hat{f}_{j},\hat{f}^{\dag}_{k}\hat{f}_{k}]=0.\nonumber \end{equation}
總的來說,我們發現引入Jordan-Wigner變換,(更明確的說是引入Jordan-Wigner弦)可以實作不同格點自旋間的對易關系.
用Jordan-Wigner變換求解XY模型
把Jordan-Wigner變換代入XY模型可以得到
\begin{eqnarray} \hat{H}_{XY}&=&-\frac{J}{2}\sum_{j}[\hat{S}_{j}^{+}\hat{S}_{j+1}^{-}+\hat{S}_{j}^{-}\hat{S}_{j+1}^{+}]\\ &=&-\frac{J}{2}\sum_{j}[\hat{f}_{j}^{\dag}e^{i\hat{\phi}_{j}}e^{-i\hat{\phi}_{j}}(1-2\hat{f}_{j}^{\dag}\hat{f}_{j})\hat{f}_{j+1}+H.c.]\\ &=&-\frac{J}{2}\sum_{j}[\hat{f}_{j}^{\dag}\hat{f}_{j+1}+\hat{f}_{j+1}^{\dag}\hat{f}_{j}] \end{eqnarray}
這樣我們發現一維量子XY模型已經變換為一維自由無自旋費米子系統.
現在,讓我們假設體系具有周期邊界條件,這意味著邊界上的最後一個自旋 \hat{S}^{\pm}_{N_{s}} (假設體系有 N_{s} 個格點)與第一個自旋 \hat{S}_{1}^{\pm} 具有交互作用
\begin{eqnarray} \hat{H}_{PBC}=-\frac{J}{2}[\hat{S}_{N_{s}}^{+}\hat{S}_{1}^{-}+\hat{S}_{N_{s}}^{-}\hat{S}_{1}^{+}]&=& -\frac{J}{2}e^{i\pi\sum_{m=1}^{N_{s}-1}\hat{f}_{m}^{\dag}\hat{f}_{m}}[\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]\nonumber\\ &=&-\frac{J}{2}e^{i\pi \hat{N}_{f}}e^{i\pi\hat{f}_{N_{s}}^{\dag}\hat{f}_{N_{s}}}[\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]\nonumber\\ &=&-\frac{J}{2}(-1)^{\hat{N}_{f}}[-\hat{f}_{N_{s}}^{\dag}\hat{f}_{1}+\hat{f}_{N_{s}}\hat{f}_{1}^{\dag}]. \end{eqnarray}
這裏我們定義了總費米子數算符 \hat{N}_{f}=\sum_{m=1}^{N_{s}}\hat{f}_{m}^{\dag}\hat{f}_{m} .註意到 \hat{N}_{f} 是守恒量,那麽 (-1)^{\hat{N}_{f}} 可以為 1 或 -1 ,前者對應 \hat{N}_{f} 為偶數,後者對應 \hat{N}_{f} 為奇數.當 \hat{N}_{f} 為偶數時, (-1)^{\hat{N}_{f}}=1 ,為了使 \hat{H}_{PBC} 具有 \hat{H}_{XY} 的形式,可以設 \hat{f}_{1}=-\hat{f}_{N_{s}+1} .同理,當 \hat{N}_{f} 為奇數時, (-1)^{\hat{N}_{f}}=-1 ,我們可設 \hat{f}_{1}=\hat{f}_{N_{s}+1} .因此,我們發現總費米子數的奇偶性決定了費米子滿足周期( \hat{f}_{1}=\hat{f}_{N_{s}+1} )或反周期( \hat{f}_{1}=-\hat{f}_{N_{s}+1} )邊界條件.
定義費米子的傅立葉變換為 \hat{f}_{j}=\frac{1}{\sqrt{N_{s}}}\sum_{k}e^{ikR_{j}}\hat{f}_{k} ,對於周期邊界我們發現( R_{j}=ja,a 為晶格間距,可設為1)
\begin{equation} \hat{f}_{1}=\hat{f}_{N_{s}+1}\Rightarrow e^{ika}=e^{ik(R_{N_{s}}+a)}\Rightarrow e^{ikN_{s}}=1 \end{equation}
這說明動量 k 可以取 k=\frac{2\pi}{N_{s}}n (n 取所有整數,即 n=0,\pm1,\pm2... ).另一方面,對於反周期邊界則有
\begin{equation} \hat{f}_{1}=-\hat{f}_{N_{s}+1}\Rightarrow e^{ikN_{s}}=-1 \end{equation}
這樣 k=\frac{2\pi}{N_{s}}n ( n 取所有半整數,即 n=\pm1/2,\pm3/2... ).因此,我們看到周期與反周期邊界條件實際上會影響動量 k 的取值,當然,在熱力學極限下 N_{s}\rightarrow\infty ,動量的取值足夠密集,此時兩者的區別可以忽略.所以,如果是尺寸很大的體系,我們可以不管兩者的區別而只采用周期邊界的形式,並且設動量取在第一布里元區,即 k\in[-\pi,\pi] .
代入傅立葉變換可得體系的哈密頓量在動量空間可以化為
\begin{eqnarray} \hat{H}_{XY}=\sum_{k}(-J\cos k)\hat{f}_{k}^{\dag}\hat{f}_{k} \end{eqnarray}
在零溫基態,費米子根據色散 -J\cos k<0 填滿 k\in[-\frac{\pi}{2},\frac{\pi}{2}] 的半個一維第一布里元區,基態波函式用費米子可以表示為
\begin{equation} |\Psi_{g}\rangle=\prod_{k<k_{F}}\hat{f}_{k}^{\dag}|0,0,0...\rangle,~k_{F}=\pi/2. \end{equation}
此時必然有 \langle \hat{f}_{k}^{\dag}\hat{f}_{k}\rangle_{T=0}=\theta(\frac{\pi}{2}-|k|) ,這樣z方向的磁化是
\begin{equation} \langle\hat{S}_{j}^{z}\rangle_{T=0}=\langle\hat{f}_{j}^{\dag}\hat{f}_{j}\rangle_{T=0}-\frac{1}{2}= \frac{1}{N_{s}}\sum_{k}\langle\hat{f}_{k}^{\dag}\hat{f}_{k}\rangle_{T=0}-\frac{1}{2}= \int_{-\pi}^{\pi}\frac{dk}{2\pi}\theta\left(\frac{\pi}{2}-|k|\right)-\frac{1}{2}=0 \end{equation}
換句話說,基態時的一維量子XY模型磁化為零,處於無序態.雖然用費米子表示的基態波函式已經寫出,但如果轉換至原始的自旋語言卻比較復雜,
\begin{eqnarray} |\Psi_{g}\rangle&=&\prod_{k<k_{F}}\frac{1}{\sqrt{N_{s}}}\sum_{j}e^{-ikR_{j}}\hat{f}_{j}^{\dag}|0,0,0...\rangle\nonumber\\ &=&\prod_{k<k_{F}}\frac{1}{\sqrt{N_{s}}}\sum_{j}e^{-ikR_{j}}\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}|\downarrow,\downarrow,\downarrow...\rangle. \end{eqnarray}
例如,考慮 N_{s}=4 ,那麽動量取值為 k=\frac{2\pi}{4}n(n=\pm\frac{1}{2},\pm\frac{3}{2}) . [5] 既然費米波向量 k_{F}=\pi/2 ,那麽基態時候占據的動量就是 k=\pm\frac{\pi}{4} .我們發現此時的基態波函式是
\begin{eqnarray} |\Psi_{g}\rangle &=&\frac{1}{\sqrt{4}}\sum_{j=1}^{4}e^{-i\frac{\pi}{4}R_{j}}\hat{S}_{j}^{+}e^{i\pi\sum_{m<j}(\hat{S}_{m}^{z}+1/2)}\frac{1}{\sqrt{4}}\sum_{j'=1}^{4}e^{i\frac{\pi}{4}R_{j'}}\hat{S}_{j'}^{+}e^{i\pi\sum_{m'<j'}(\hat{S}_{m'}^{z}+1/2)}|\downarrow,\downarrow,\downarrow,\downarrow\rangle\nonumber\\ &=&\frac{1}{4} (e^{-i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{-i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)}+ e^{-i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)}+ e^{-i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)})\nonumber\\ &\times&(e^{i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)} +e^{i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)} +e^{i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)}) |\downarrow,\downarrow,\downarrow,\downarrow\rangle\nonumber\\ &=&\frac{1}{4} (e^{-i\frac{\pi}{4}}\hat{S}_{1}^{+} +e^{-i\frac{\pi}{4}2}\hat{S}_{2}^{+}e^{i\pi(\hat{S}_{1}^{z}+1/2)}+ e^{-i\frac{\pi}{4}3}\hat{S}_{3}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+1)}+ e^{-i\frac{\pi}{4}4}\hat{S}_{4}^{+}e^{i\pi(\hat{S}_{1}^{z}+\hat{S}_{2}^{z}+\hat{S}_{3}^{z}+3/2)})\nonumber\\ &\times&(e^{i\frac{\pi}{4}}|\uparrow,\downarrow,\downarrow,\downarrow\rangle +e^{i\frac{\pi}{4}2}|\downarrow,\uparrow,\downarrow,\downarrow\rangle +e^{i\frac{\pi}{4}3}|\downarrow,\downarrow,\uparrow,\downarrow\rangle +e^{i\frac{\pi}{4}4}|\downarrow,\downarrow,\downarrow,\uparrow\rangle). \end{eqnarray}
完成上述計算可以看到 |\Psi_{g}\rangle 包含6項:
\begin{eqnarray} |\Psi_{g}\rangle &=&\frac{i}{2}\sin\frac{\pi}{4}(|\uparrow,\uparrow,\downarrow,\downarrow\rangle+|\downarrow,\uparrow,\uparrow,\downarrow\rangle)\nonumber\\ &+&\frac{i}{2}\sin\frac{2\pi}{4}(|\downarrow,\uparrow,\downarrow,\uparrow\rangle+|\uparrow,\downarrow,\downarrow,\uparrow\rangle)\nonumber\\ &+&\frac{i}{2}\sin\frac{3\pi}{4}(|\uparrow,\downarrow,\uparrow,\downarrow\rangle+|\downarrow,\downarrow,\uparrow,\uparrow\rangle)\nonumber. \end{eqnarray}
這種不同自旋構型之間的高度混合是零溫磁性無序態的典型特征,用現代的語言來說就是所謂的量子自旋液體態.
為了便於參考,體系的基態能密度是
\begin{equation} \frac{E_{g}}{N_{s}}=\frac{1}{N_{s}}\sum_{k}-J\cos k\theta(J\cos k)=\int_{-\pi/2}^{\pi/2}\frac{dk}{2\pi}(-J\cos k)=-\frac{J}{\pi}. \end{equation}
高維Jordan-Wigner變換的困難
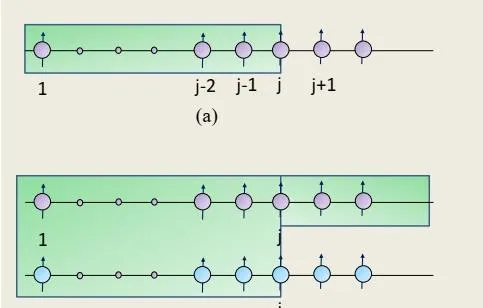
在結束這一小節的討論前,讓我們感受一下一維Jordan-Wigner變換直接推廣到高維的困難.為簡單起見,我們考慮兩個耦合的XY模型所組成的自旋雙鏈,這可以看作是二維系統的一維極限,
\begin{equation} \hat{H}=-\frac{J_{1}}{2}\sum_{j}[\hat{S}_{aj}^{+}\hat{S}_{aj+1}^{-}+\hat{S}_{aj}^{-}\hat{S}_{aj+1}^{+}] -\frac{J_{2}}{2}\sum_{j}[\hat{S}_{bj}^{+}\hat{S}_{bj+1}^{-}+\hat{S}_{bj}^{-}\hat{S}_{bj+1}^{+}]-\frac{w}{2}\sum_{j}[\hat{S}_{aj}^{+}\hat{S}_{bj}^{-}+\hat{S}_{aj}^{-}\hat{S}_{bj}^{+}] \end{equation}
這裏指標 a,b 分別代表第一和第二個XY自旋鏈, J_{1},J_{2} 是鏈內的XY耦合,w是鏈間耦合.仿照一維XY模型的處理,我們可以假象把第二條自旋鏈直接拼接到第一條鏈的末端而形成等效的一維鏈,這樣就可以套用Jordan-Wigner變換的基本形式,即有:
\begin{eqnarray} &&\hat{S}_{aj}^{+}=\hat{f}_{aj}^{\dag}e^{i\hat{\phi}_{aj}},~~\hat{\phi}_{aj}=\pi\sum_{1\leq m<j}\hat{f}_{am}^{\dag}\hat{f}_{am},~~\hat{S}_{aj}^{z}=\hat{f}_{aj}^{\dag}\hat{f}_{aj}-\frac{1}{2}\nonumber\\ &&\hat{S}_{bj}^{+}=\hat{f}_{bj}^{\dag}e^{i\hat{\phi}_{bj}},~~\hat{\phi}_{bj}=\pi\sum_{m}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm},~~\hat{S}_{bj}^{z}=\hat{f}_{bj}^{\dag}\hat{f}_{bj}-\frac{1}{2}\nonumber \end{eqnarray}
註意到第二個自旋鏈的每個相位因子 \hat{\phi}_{bj} 感受同一個自旋鏈上自旋的影響還會受到第一個自旋鏈的影響,即 \pi\sum_{m}\hat{f}_{am}^{\dag}\hat{f}_{am} .把這個變換代入模型可得
\begin{eqnarray} \hat{H}&=&-\frac{J_{1}}{2}\sum_{j}[\hat{f}_{aj}^{\dag}\hat{f}_{aj+1}+h.c.] -\frac{J_{2}}{2}\sum_{j}[\hat{f}_{bj}^{\dag}\hat{f}_{bj+1}+h.c.]\nonumber\\ &-&\frac{w}{2}\sum_{j}[\hat{f}_{aj}^{\dag}e^{i(\pi\sum_{m\geq j}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm})}\hat{f}_{bj}+h.c.] \end{eqnarray}
我們發現描述自旋鏈耦合的 w 項出現了難以處理的費米子算符的指數形式 e^{i(\pi\sum_{m\geq j}\hat{f}_{am}^{\dag}\hat{f}_{am}+\pi\sum_{1\leq m<j}\hat{f}_{bm}^{\dag}\hat{f}_{bm})} ,這是從a自旋鏈上j格點到b自旋鏈j格點的Jordan-Wigner弦.顯然,一般的二維自旋模型可以看作很多不同的一維自旋鏈的耦合,由於不同鏈間Jordan-Wigner弦的存在,自旋模型無法變換為簡單的自由費米子問題而成為交互作用費米子問題,這就是Jordan-Wigner變換直接高維推廣所面臨的基本困難.
參考
- ^ U(1)/O(2)表明自旋繞著z軸轉動不變
- ^ 定義一個量子力學問題需要定義Hilbert空間以及算符
- ^ Jordan,Wigner,About the Pauli exclusion principle,Z.Phys. 47,631(1928)這文章是用德文寫的,看不懂!
- ^ 一般會包換規範場型別的自由度以及費米子自由度
- ^ 這裏是費米子取反周期邊界










