補充一下。
以一維自旋鏈為例,JW變換具體的形式是:
\begin{equation} \begin{aligned} c_i^{\dagger}&=\prod_{l<j}\sigma_l^z \sigma_j ^- \\ c_i&=\prod_{l<j}\sigma_l^z\sigma_j^+ \end{aligned} \end{equation}
可以看出其形式是自旋鏈乘上某點的自旋升降算符。
其中, \sigma^-_i 和 \sigma^+_i 是自旋的升降算符, c^{\dagger}_i 和 c_i 是費米子的產生湮滅算符,題主可以自己檢驗一下, c^{\dagger}_i 和 c_i 滿足費米子的反對易關系。第i個格點上的粒子數算符是:
\begin{equation} c_i^\dagger c_i=\sigma_i^-\sigma_i^+=\frac{1-\sigma_i^z}{2} \end{equation}
那麽 \begin{equation} \sigma_i^z=1-2c^\dagger_i c_i \end{equation}
可以看到某個格點上的自旋狀態 |\uparrow\rangle 和 |\downarrow\rangle 分別對應著fermion占據數為0和1的狀態。
凝聚態裏經常用JW變換結合Fourier變換和Bogoliubov變換來求解某個自旋體系的能譜,之前了解過幾份工作用到了這套手續,題主感興趣的話可以看一下:
附上之前算過的某個spin模型的能譜和完全數值結果的對比圖(小系統):
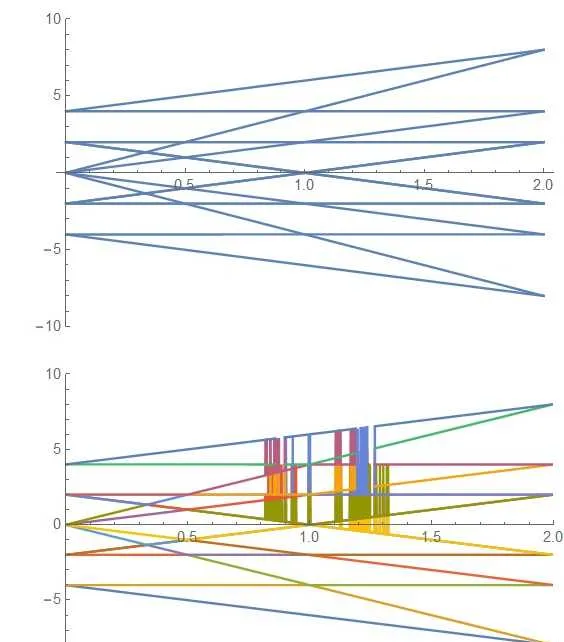
橫軸是模型的某個參數。上圖是精確解,下圖是數值計算的結果(直接mma求矩陣本征值),我也搞不清楚那一堆豎線是什麽情況= =










